Tema III. Movimiento de un cuerpo
En mecánica, el movimiento es un cambio de la posición
de un cuerpo a lo largo del tiempo respecto de un sistema de referencia.
Mecánica:
Es la rama de la física que estudia y analiza el movimiento y reposo de los
cuerpos, y su evolución en el tiempo, bajo la acción de fuerzas. Esta se divide
en tres:
1. Cinemática: Podemos
definirla como una rama de la física que estudia el movimiento de los cuerpos
en el espacio, independientemente de las causas que lo producen. Por lo tanto
se encarga del estudio de la trayectoria en función del tiempo.
2. Dinámica:
Es la parte de la física que estudia la relación existente entre las fuerzas
que actúan sobre un cuerpo y los efectos que se producirán sobre el movimiento
de ese cuerpo.
3. Estática: Es
la rama de la mecánica clásica que analiza las cargas (fuerza, par / momento) y
estudia el equilibrio de fuerzas en los sistemas físicos en equilibrio
estático, es decir, en un estado en el que las posiciones relativas de los
subsistemas no varían con el tiempo.
Desplazamientos
Tipos de movimientos
Desplazamientos
·
Desplazamiento:
es el vector que define la posición de un punto o partícula en relación a un
origen A con respecto a una posición B. El vector se extiende desde el punto de
referencia hasta la posición final. Cuando se habla del desplazamiento en el
espacio solo importa la posición inicial y la posición final, ya que la
trayectoria que se describe no es de importancia.
·
Velocidad:
es la magnitud física que expresa la variación de posición de un objeto en
función del tiempo, o distancia recorrida por un objeto en la unidad de tiempo.
Se suele representar por la letra V. La
velocidad puede distinguirse según el lapso considerado, por lo cual se hace
referencia a la velocidad instantánea, la velocidad promedio, etcétera. En el
Sistema Internacional de Unidades su unidad es el metro por segundo (m/s). Se
divide en dos:
Ø Se define la velocidad
instantánea como el límite de la velocidad media cuando el intervalo de
tiempo considerado tiende a 0. También se define como la derivada del vector de
posición respecto al tiempo. Su expresión viene dada por:
Ø Se define la velocidad media de un cuerpo que se mueve entre dos puntos P1 y P2
como el cociente entre el vector desplazamiento y el intervalo de tiempo en que
transcurre el desplazamiento. Su expresión viene dada por:
·
Aceleración: es
una magnitud vectorial que nos indica la variación de velocidad por unidad de
tiempo. En el Sistema
Internacional de Unidades su unidad es el metro por segundo cuadrado (m/s2).
Se divide en dos:
Ø Se define la aceleración
instantánea, como el límite de la aceleración media cuando el intervalo de
tiempo considerado tiende a 0. También se define de manera equivalente como la
derivada de la velocidad respecto al tiempo. Su expresión viene dada por:
Ø Se define la aceleración
media entre dos puntos P1 y P2 como
la división de la variación de la velocidad y el tiempo transcurrido entre
ambos puntos:
Tipos de movimientos
1- Movimiento rectilíneo: Cuando
la trayectoria de un móvil es recta, la velocidad lleva siempre esa misma
dirección. A este tipo de movimiento lo llamamos movimiento rectilíneo.
Ejemplos de los tipos de movimiento rectilíneo más importantes:
Ø
Las ecuaciones del movimiento rectilíneo
uniforme son:
X
= X0 + V⋅T ;
V = V0 = cte ; a =0
Donde:
- X, X0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m).
- V,V0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional (S.I.) es el metro por segundo (m/s).
- a: La aceleración del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2).
2- Movimiento rectilíneo uniformemente
variado: Tiene una trayectoria recta y su aceleración es constante; es decir, aumenta y disminuye de manera
constante.
El
movimiento rectilíneo uniformemente variado puede ser acelerado o retardado.
Ø
Movimiento rectilíneo uniformemente acelerado: Es
acelerado cuando su velocidad aumenta a medida que transcurre el tiempo y, por
tanto, la aceleración es positiva.
El
cohete, al despegar, pasa de estar en reposo a adquirir una enorme velocidad.
Además, como la trayectoria que realiza es una línea recta, decimos que el
cohete lleva un movimiento rectilíneo uniformemente acelerado.
Además de movimientos, tenemos la velocidad y aceleración
de dicho movimiento:
ü
Velocidad
en función del tiempo: la velocidad varía proporcionalmente al tiempo,
por lo que la representación gráfica v-t (velocidad en función del tiempo) es
una recta ascendente.
ü
Aceleración
en función del tiempo: tal como lo dice su nombre, en el Movimiento
uniformemente acelerado la aceleración es constante, por lo que la gráfica a-t (aceleración
en función del tiempo) es una recta paralela al eje del tiempo, por encima de
esta (la fuerza responsable de la aceleración es constante) .
Ø Movimiento rectilíneo uniformemente retardado: Es retardado cuando su
velocidad disminuye a medida que pasa el tiempo y, por tanto, la aceleración es
negativa.
Además
de movimientos, tenemos la velocidad y aceleración de dicho movimiento:
ü Velocidad en función del tiempo: en
un movimiento uniformemente decelerado o retardado su pendiente disminuye de un
modo uniforme, lo que da lugar a una gráfica velocidad-tiempo decreciente y
rectilínea.
ü Desaceleración en función del tiempo:
en este tipo de movimientos la desaceleración es constante, por lo que la
gráfica a-t (en este caso desaceleración en función del tiempo) es una recta
paralela al eje del tiempo, por debajo de esta.
3- Movimientos curvilíneos: si la trayectoria del móvil es una línea
curva, la velocidad lleva siempre la dirección tangente a la trayectoria en
cada punto. En este caso hablamos de
movimientos curvilíneos. Ejemplos:
Ø Circular:
la trayectoria del móvil es una circunferencia. Si lo que gira da siempre el
mismo número de vueltas por segundo, decimos que posee movimiento circular
uniforme (MCU). Ejemplo:
§ Las
aspas de los aerogeneradores de los parques eólicos realizan un movimiento
circular.
§ -
Un disco compacto durante su reproducción en el equipo de música, las
manecillas de un reloj o las ruedas de una motocicleta.
Ø Parabólico:
La trayectoria del móvil es una parábola. Este movimiento se descompone en un
movimiento horizontal y uno vertical. Ejemplo:
§ -
El movimiento que realiza la jabalina al ser lanzada.
§ -
El lanzamiento de pelotas u otros objetos en la mayoría de los deportes.
Ø Elíptico:
es un caso de movimiento acotado en el que una partícula describe una
trayectoria elíptica. Ejemplo:
§ La
Tierra, al igual que el resto de los planetas del sistema solar, gira al
rededor del sol describiendo una órbita elíptica.
Ø Movimiento pendular:
La trayectoria del móvil es una circunferencia; pero el móvil no cae. Es un
movimiento de vaivén; por ejemplo, el movimiento de un columpio.
Formulas Cinemática
CINEMATICA
4-
Movimientos especiales:
Ø Caída libre:
cualquier cuerpo soltado desde cierta altura es atraído por la fuerza de
gravitación que ejerce la Tierra y cae hacia el suelo siguiendo una trayectoria
recta. Este movimiento se denomina caída libre y es un ejemplo particular del
movimiento rectilíneo uniformemente acelerado.
- Si despreciamos los efectos del aire en la caída de los cuerpos, todos los cuerpos caen con una aceleración constante, independientemente de su masa, forma o tamaño.
- La aceleración que adquieren los cuerpos cuando caen se denomina aceleración de la gravedad o aceleración gravitacional. Se la simboliza con la letra g.
- El valor de la aceleración de la gravedad depende del lugar de la Tierra en que se mida. Así, mientras más lejos se encuentre un cuerpo del centro de la Tierra, menor será la aceleración de la gravedad. El valor promedio de la aceleración de la gravedad en la superficie terrestre es de 9,8 m/s2.
Ø Lanzamiento vertical:
cuando lanzas un cuerpo hacia arriba (por ejemplo, una moneda), este asciende
con un movimiento rectilíneo durante cierto tiempo y, luego, cae.
- Cuando la moneda alcanza el punto más alto de su trayectoria rectilínea, esta se encuentra momentáneamente con velocidad cero y se invierte el sentido del movimiento: se mueve cayendo libremente desde esa altura.
- En el lanzamiento de un cuerpo hacia arriba, se pueden distinguir dos movimientos: el movimiento vertical hacia arriba, con velocidad inicial conocida, y el movimiento vertical hacia abajo, que se puede entender como un movimiento de caída libre con velocidad inicial cero.
- Tanto al subir como al bajar, el cuerpo mantiene el mismo valor de la aceleración gravitatoria. Al ascender, esta hace decrecer la velocidad, y al descender, la aumenta.
5-
Movimiento circular: es el que se basa en un eje de giro y
radio constante, por lo cual la trayectoria es una circunferencia. Si además,
la velocidad de giro es constante (giro ondulatorio), se produce el movimiento
circular uniforme, que es un caso particular de movimiento circular, con radio,
centro fijo y velocidad angular constante.
En el movimiento circular
hay que tener en cuenta algunos conceptos básicos para la descripción
cinemática y dinámica del mismo:
1.
Eje
de giro: es la línea recta alrededor de la cual se realiza la
rotación, este eje puede permanecer fijo o variar con el tiempo pero para cada
instante concreto es el eje de la rotación (considerando en este caso una
variación infinitesimal o diferencial de tiempo). El eje de giro define un
punto llamado centro de giro de la trayectoria descrita (O).
2.
Arco:
partiendo de un centro fijo o eje de giro fijo, es el espacio recorrido en la
trayectoria circular o arco de radio unitario con el que se mide el
desplazamiento angular. Su unidad es el radián (espacio recorrido dividido
entre el radio de la trayectoria seguida, división de longitud entre longitud,
adimensional por tanto).
En dinámica de los
movimientos curvilíneos, circulares y/o giratorios se tienen en cuenta además
las siguientes magnitudes:
1.
Momento
angular (L): es la magnitud que en el movimiento rectilíneo
equivale al momento lineal o cantidad de movimiento pero aplicada al movimiento
curvilíneo, circular y/o giratorio (producto vectorial de la cantidad de
movimiento por el vector posición, desde el centro de giro al punto donde se
encuentra la masa puntual).
2.
Momento
de inercia (I): es una cualidad de los cuerpos que
depende de su forma y de la distribución de su masa y que resulta de
multiplicar una porción concreta de la masa por la distancia que la separa al
eje de giro.
3.
Momento
de fuerza (M): o par motor es la fuerza aplicada por la
distancia al eje de giro (es el equivalente a la fuerza agente del movimiento
que cambia el estado de un movimiento rectilíneo).
Ø Movimiento circular uniforme (M.C.U.):
es
un movimiento de trayectoria circular en el que la velocidad angular es
constante. Esto implica que describe ángulos iguales en tiempos iguales. En él,
el vector velocidad no cambia de módulo pero sí de dirección (es tangente en
cada punto a la trayectoria). Esto quiere decir que no tiene aceleración
tangencial ni aceleración angular,
aunque sí aceleración normal.
Características del Movimiento
Circular Uniforme (M.C.U.):
ü La
velocidad angular es constante (ω = cte).
ü El
vector velocidad es tangente en cada punto a la trayectoria y su sentido es el
del movimiento. Esto implica que el movimiento cuenta con aceleración normal.
ü Tanto
la aceleración angular (α) como la aceleración tangencial (at) son nulas, ya
que la rapidez (módulo del vector velocidad) es constante.
ü Existe
un periodo (T), que es el tiempo que el cuerpo emplea en dar una vuelta
completa. Esto implica que las características del movimiento son las mismas
cada T segundos. La expresión para el cálculo del periodo es T=2π/ω y es sólo
válida en el caso de los movimientos circulares uniformes (m.c.u.).
ü Existe
una frecuencia (f), que es el número de vueltas que da el cuerpo en un segundo.
Su valor es el inverso del periodo.
Ø Movimiento circular uniformemente
acelerado (M.C.U.A.): se presenta cuando una partícula o
cuerpo sólido describe una trayectoria circular aumentando o disminuyendo la
velocidad de forma constante en cada unidad de tiempo. Es decir, la partícula
se mueve con aceleración constante.
ü Posición: es
más rápido o más lento según avanza el tiempo. El ángulo recorrido (θ) en un intervalo
de tiempo t se calcula por la siguiente fórmula:
ü Velocidad angular: aumenta
o disminuye linealmente cuando pasa una unidad del tiempo. Por lo tanto,
podemos calcular la velocidad angular en el instante t como:
ü
Velocidad tangencial: es el producto de la
velocidad angular por el radio r. La velocidad tangencial también se incrementa
linealmente mediante la siguiente fórmula:
ü Aceleración angular:
en el movimiento circular uniformemente acelerado es constante. Se calcula como
el incremento de velocidad angular ω desde el instante inicial hasta el final
partido por el tiempo.
ü Aceleración tangencial:
en el movimiento circular uniformemente acelerado MCUA se calcula como el
incremento de velocidad
desde
el instante inicial hasta el final partido por el tiempo.
ü
ü Período: En
el MCUA la velocidad angular cambia respecto al tiempo. Por tanto, el período cada vez será menor o mayor
según si decrece o crece la velocidad angular.
ü
Frecuencia: en
el caso del MCUA es mayor o menor porque la velocidad angular cambia. La
fórmula de la frecuencia será:
Formulas Cinemática
CINEMATICA
Demostración
de ecuaciones:
1.
Vx = Vox + a.t
2.
X = Xo + Vox.t + at²
3.
Vx² = Vox² + 2a (X-Xo)
4.
X – Xo = t
DEMOSTRACION
FORMULA 1
a = despejamos a * ∆t = ∆v
a (t-0) = Vx
– Vox
at
+ Vox = Vx
DEMOSTRACION
FORMULA 2
El desplazamiento ∆x se
obtiene a partir del cálculo del área por debajo de la gráfica
velocidad-tiempo.
∆x
= Área del rectángulo + Área del triangulo
b
x h +
∆x
= Vo.∆t +
Considerando que si a = despejamos a * ∆t = ∆v y
reemplazamos en la ecuación anterior.
∆x = Vo.∆t +
X - Xo = Vo.t +
De lo que finalmente obtenemos:
X
= Xo + Vox.t + ½ at²
DEMOSTRACION
FORMULA 3
A partir de la primera
ecuación Vx = Vox + at, ya demostrada.
Despejamos: t = y reemplazamos en X = Xo + Vox.t + ½
at².
X
= Xo + Vox + ½ a
X
- Xo = + ½ a
X
- Xo = +
X
– Xo = (VoxVx - Vox²) +
X
– Xo = (- Vox²) +
X
– Xo = (- Vox²) +
X
– Xo =
X
– Xo = (Vx² - Vox²)
(X
– Xo)2a = Vx² - Vox²
(X
– Xo)2a + Vox² = Vx²
Vx² = Vox² + 2a (X
– Xo)
DEMOSTRACION
FORMULA 4
Partiendo de la 1ra
ecuación Vx = Vox + at, ya demostrada.
Despejamos:
a = y reemplazamos en X = Xo + Vox.t + ½ at².
X
= Xo + Vox.t + ½ t²
X
- Xo = Vox.t + ½ (Vx – Vox) t
X
- Xo = Vox.t + t
X - Xo = t


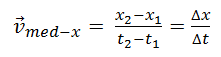


























No hay comentarios:
Publicar un comentario